- 作者:佚名
- 发表时间:2024-07-01 13:59
我是搞图像处理的硕士生。我看到中大的研究生都有一本《凸优化 Stephen Boyd等著》,于是也买了本,想系统学一学。虽然我也在本校上了最优化的课,但还是觉得有必要多学些。我听网上説这本书是入门级的书籍,书封面还写着信息技术和电气工程学科的教材。但我怎么觉得看第二章的时候就看晕了,优化的部分都还没看到,一大堆概念感觉很多都不会。。。。。网上搜了下説要先有泛函的知识才能看得懂。是真的吗?这本书该怎么自学?有什么学习方法求推荐!
最优化方面的书籍当然首推Stephen Boyd 和Lieven Vandenberghe合著的《Convex Optimization》了,书籍内容详实,配备资料丰富,口碑爆棚。光看书比较枯燥,应该结合视频一起学习,下面分享的第一个部分就有视频链接,如果失效了,可以在评论区说一声,我后面更新。以下推荐的其他书籍感兴趣的话,也可以看看哈,没时间的话,看第一个就可以了。如果觉得有帮助,可以点赞鼓励哟^_^
书籍-链接:https://pan.baidu.com/s/1ha17u_EHT2Luu2heeGR2Jw 提取码:jd1f
视频-链接:https://pan.baidu.com/s/1KOENOziKrOfNprTpLnvSQw 提取码:22cx
幻灯片-链接:https://pan.baidu.com/s/1tzsEln1kTOl9KbjQFXniww 提取码:qhcx
习题答案-链接:https://pan.baidu.com/s/1EVvcn9LnoOfeutAkk9ExJQ 提取码:yq2j

链接:https://pan.baidu.com/s/1-fWnG0_TlIuXB69t9Bnymg 提取码:cypn

链接:https://pan.baidu.com/s/1Xn9CTMDZydB0SaUSpmXmBg 提取码:iqwe

链接:https://pan.baidu.com/s/10DJr0FAeIHp9iDdJjnRS7w 提取码:ax1z

链接:https://pan.baidu.com/s/16VVgOXOIgzlfRvtIaPgi7Q 提取码:s3xs

链接:https://pan.baidu.com/s/1dzl7Tfee9SfbEfgRroDd5A 提取码:6o0w

链接:https://pan.baidu.com/s/1it4ILDGG3rRJf-GazFZUQA 提取码:8lkw

链接:https://pan.baidu.com/s/1KP19Ppn1ssqUezAw7TFiEg 提取码:ipem

链接:https://pan.baidu.com/s/1ulUUw6zJJGPAf7SkZoAfTA 提取码:e9vq

链接:https://pan.baidu.com/s/1wQ5WmiQ1LbARShv6kWyx6A 提取码:9ggb

链接:https://pan.baidu.com/s/1EdTbtJ5s296WIeZaS3wIpw 提取码:w7zg

链接:https://pan.baidu.com/s/1xOWfFzUI0CnXsx9qOf0lWQ 提取码:5kdi

链接:https://pan.baidu.com/s/134WM2SnoJhhHko2adC2Wzg 提取码:11rf

对于使用anaconda的人来说,可按照下面步骤安装,亲测有效!
首先安装[Visual Studio build tools for Python 3]
然后激活虚拟环境,使用命令安装
conda install -c conda-forge cvxpyPython: Pyomo, CVXPY
Julia: JuMP, Convex.jl
MATLAB: YALMIP, CVX
机器学习/数据科学-核心/进阶免费书籍机器学习/数据科学-免费Python书籍最优化免费书籍-专题Books for Causal Inference 因果推断免费书籍 (R2,持续更新)Causal Inference Courses 因果推断免费课程(R3, 持续更新)
22年更新一下回答,Boyd的凸优化前四章其实算是「凸分析」了,讲的都是凸优化里面很理论的东西,但讲道理,只算是 intermediate level,对于非OR专业的研究生来说基本上也够了;但是,现在我还是建议OR专业的研究生不必过分认真读Boyd的这本书(因为据说Boyd本身数学也不好),凸分析只看这本书是远远不够的,可以先拿这本书入门,大致了解一下凸优化包含了哪些理论,关于共轭函数、对偶等更深的知识,我个人比较推荐阅读 Bersekas 的 《convex optimization theory》,国内买得到这本书的影印版,想要这本书pdf的可以私信我。
从我大三下学习开始读 Boyd cvxopt 开始计算,到现在应该过去一年半了。
我差不多把这本书正文的 80% 以上给看下来了,下面谈一点看法。
这本书分为三个部分,第一部分是理论,包括凸集、凸函数、对偶理论等,可以说是这本书最精华的部分了,非常建议认真阅读。刚开始可能有点难,多读几遍就好了,一些知识可能也不是很重要,第一遍看的时候略过就行了。
读的时候,也可以有所取舍。一般SDP、SOCP的部分可以先略过,主要抓凸分析和对偶这两块知识。比较建议第二、第三遍看的时候好好钻研一下书上的例子。
但是,坦白说,我认为,所有关于锥规划的部分,这本书写的都不太好,我是看了叶老师的 Linear and Nonlinear Programming 的锥线性规划那一章才知道锥规划是要干什么。当然,我必须说的是,对于专门从事运筹优化学习、研究的人来讲,锥是一个非常非常重要的东西,只是其重要性在Boyd书的第一部分几乎就没有体现出来,所以会让人感到头大。如果不想死磕优化,学这个只是为了应付机器学习,锥的部分跳过不学完全没有问题。
第二部分是一些实际应用,讲真看这一部分的时候我是非常震惊的,没想到那么多问题都能被优化工具给轻松解决,尤其是统计那一章,用SDP去估计一个随机向量在凸集上的概率的界;另外还涉及了很多与机器学习相关的优化问题。
这一部分的许多例子都涉及了超出书籍的知识,比如 robust optimization,semi-infinite programming,都能在书上找到影子。
第三部分是算法,这也是传统凸优化的知识,但是相比前面两部分价值就没有那么大了。关于优化算法我还是推荐叶老师的 Linear and Nonlinear Programming 后两部分。
另外,如果想专门从事运筹优化方向的话,这本书确实只是入门。
Boyd 的《Convex Optimization》确实是一本好书,当年在数学系读书的时候,很多老师也都推荐这本书。这本书的优点是大而全,拿在手上就能感受到沉甸甸的重量。。。我自己也曾经想好好读一读这本书,尝试了几次都没有完整地坚持下来。。
究其原因在于,对于初学者来说,如此厚重的书有时却不一定友好,因为不知道哪些东西该跳过(或者可以跳过),只能硬着头皮从头看到尾,生怕错过了什么重要部分。但书本身又太厚重,花费很多时间,结果才发现看了1/10,很容易坚持不下去。于是就出现了题主所说的“看第二章的时候就看晕了,优化的部分都还没看到,一大堆概念感觉很多都不会”。。
其实如果不是专业研究运筹学或者优化理论,不太需要把整本书完整的看下来,也不需要去看太多专业的优化书籍。
这里强烈推荐 CMU 的青年才俊 Ryan Tibshirani 开设的《Convex Optimization》的课程。Ryan 是统计系的老师,开设这门课也主要是面向机器学习研究的同学,所以很适合机器学习领域的同学学习该课程。
看 Boyd 的书以及看 Boyd 的视频都没坚持下来的我,竟然把这门课完整地看下来了。一是这门课比较精简,并不需要花太多时间在上面,学习起来比较有动力;二是因为 Ryan 是个非常好的老师,绝不是照本宣科那种。尽管看上去非常年轻,但是非常循循善诱,讲课的功底非常好。说实话,这么多年,我遇到过的能把数学课讲得深入浅出的,一个手都能数得过来。Ryan 就是其中一个。
这门课从比较基础的地方讲起,并不需要太多预备知识,像题主所说的泛函分析完全不需要。尽管有公式推导,也有收敛性和收敛速度证明这些。本来我之前看书看到这些东西也头大,在 Ryan 的讲解下却听懂了!!
这门课的主页在http://www.stat.cmu.edu/~ryantibs/convexopt/,里面有上课时用的 slides,还有Note,在 YouTube 上还有当年上课时录的视频。
我当年看的应该是2016年的版本,现在好像有更新的。
Ryan 的英语比较纯正,没什么口音,配合 YouTube 的字幕和 slides 看,听懂问题不大。不过课程后半段有个印度裔老师,说的英语我就听得不太懂。。靠着看 slides 也坚持了下来。
课程最后也会请一些嘉宾(Guest Lecture)来讲讲跟课程相关的比较前沿的东西,我当年看的时候,请的一个嘉宾来讲了 SGD 的一些相关算法,像是什么 SVRG,SAGA 这种算法,直接看论文都不太看得明白,也在这门课上听懂了。
这里附上这门课的目录,有兴趣的同学可以看看。这门课基本覆盖了机器学习里面能用到的优化算法,像是 SVM 里面需要用到的 Duality,以及很多基于梯度的优化算法。学完这门课,基本上机器学习相关论文里遇到的优化部分都没太多问题。
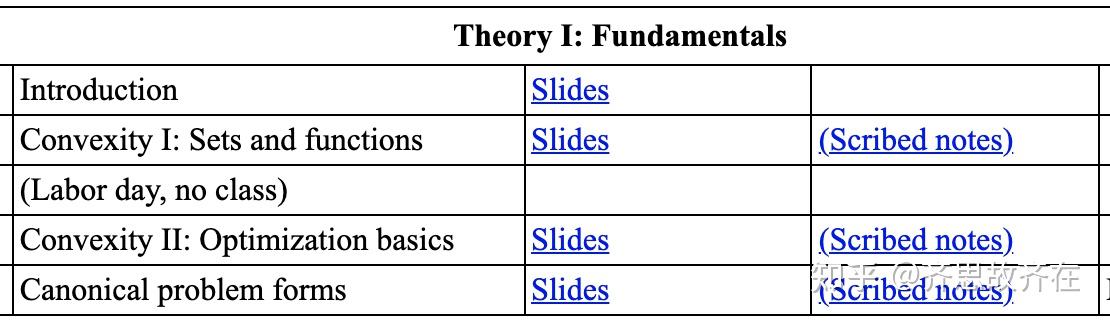
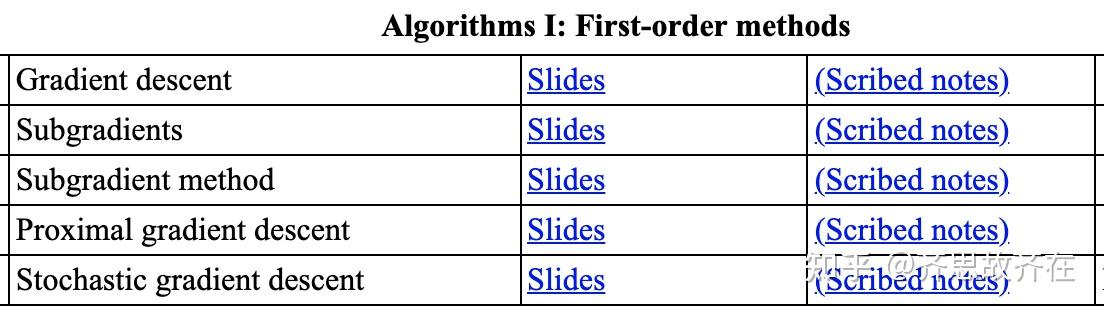
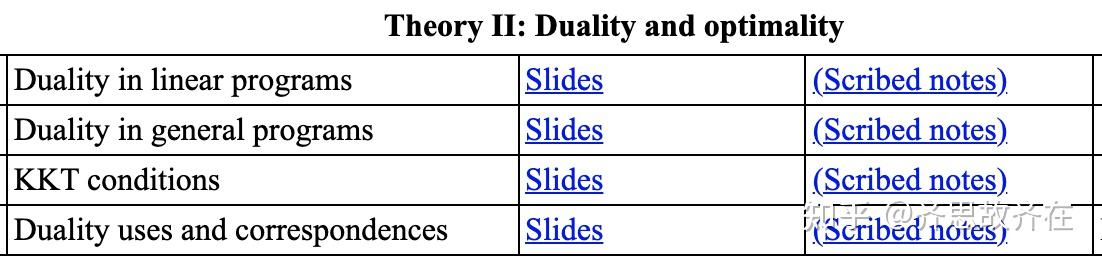
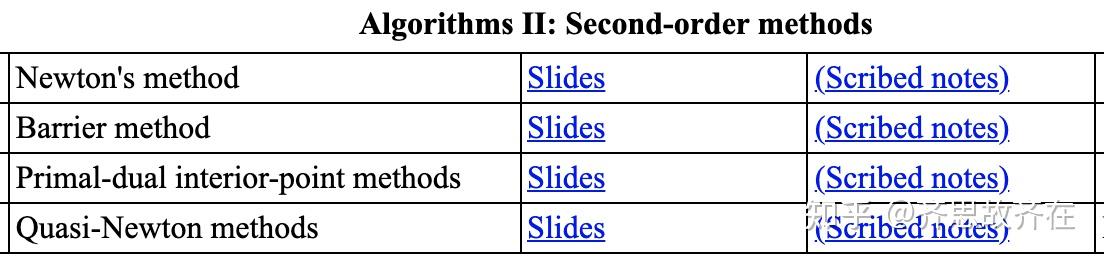
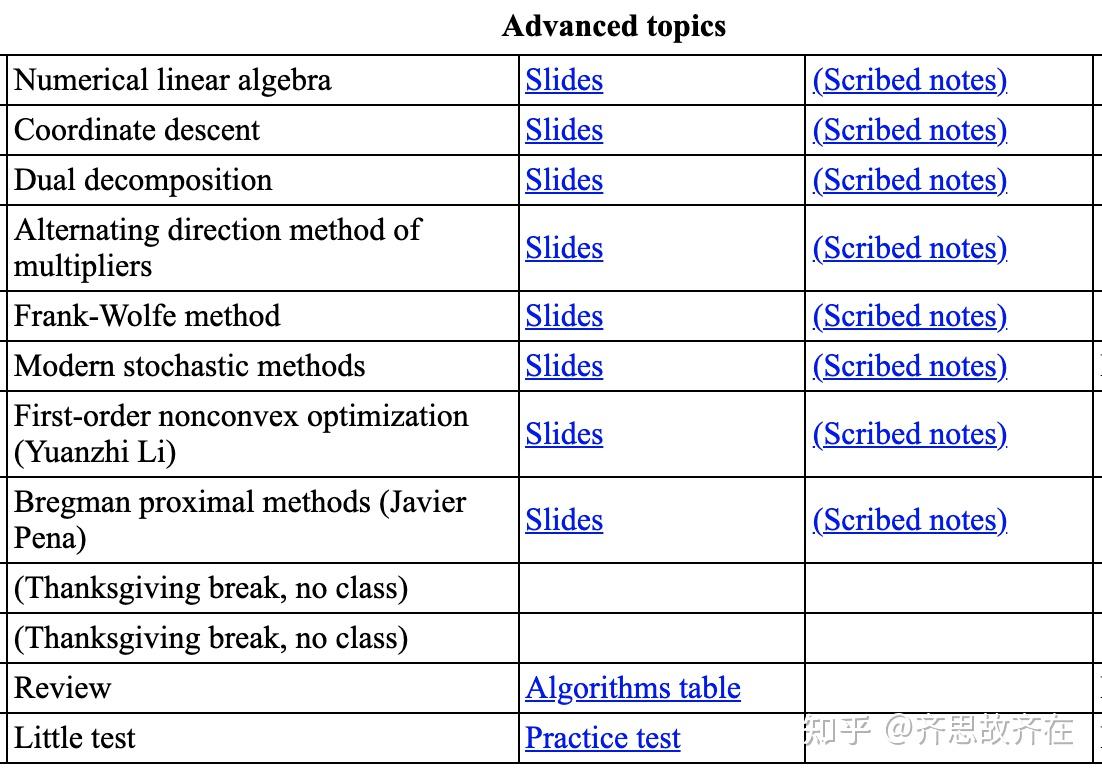
国外其实有很多不错的公开课,也有很多非常年轻的老师讲课水平非常好,像是 Stanford 的Richard Socher (当年看他讲的NLP入的门)和 MIT 的 Erik Demaine (他讲的算法课非常好)都是非常年轻,但是讲课水平极高。
本课程整理自中国科学技术大学2011年课程《最优化理论》,
- 主讲人:凌青老师
https://cse.sysu.edu.cn/content/3112
- 课程主要教材
Boyd S , Vandenberghe L . Convex Optimization. Cambridge University Press, 2004.
https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf
- 课程视频网上有很多,这里只放一个链接
https://www.bilibili.com/video/BV1Jt411p7jE
- 本文彩色插图由 @陌上疏影凉 提供
- 本教程已收录到专栏
- 本文内容对应视频lec21-24,本文对应2个知识点,分别为
- 优化问题
- 凸优化问题
- convex problems:目标函数为凸函数,约束为凸集(广义)
- 优化问题常写为如下形式:
?
? :优化变量(optimization variable)
? :目标函数/损失函数(objective function/cost function)
? 取最大值时,这个函数也叫作效用函数(utility function)
? :不等式约束(inequality constraint)
? :等式约束(equality constraint)
? 时,无约束(unconstrained)优化问题
? 优化问题的域:domain
?
- 可行解集(feasible set)
为可行解:满足所有约束的点集合,记为
- 问题的最优值(optimal value)
- 最优解(optimal point/solution)
若,且
- 最优解集(optimal set)
次优解集(
-suboptimal set)
satisficing solution 足够满意解
- 局部最优解(local optimal)
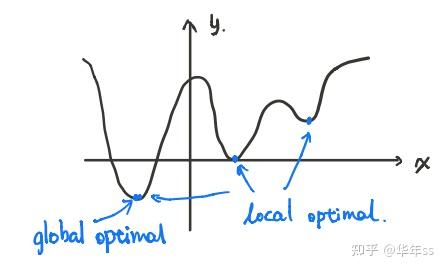
- 几个集合之间的关系
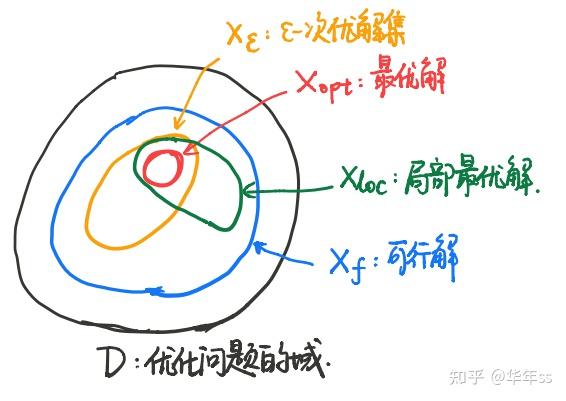
- box constraints
- 等价问题(equivalence),如果解了一个问题,可以立即得到另一个问题的解,反过来也成立,则称这两个问题是等价问题
- 对标准形式进行放缩
?
其中所有,所有
。这只是对原问题的目标函数与约束进行了放缩,显然与原问题等价
- 函数嵌套
函数单调递增,仅当
,仅当
时,
则如下问题与标准问题等价
?
- 当目标函数为误差2范数时,在目标函数上加平方,问题等价不变
<==>
- 消除等式约束,假设
满足约束
,则原问题可写为
- 消除线性等式约束
可以将线性等式约束视为线性方程组,先解出线性方程组的解,然后带入原优化问题
- 狭义的凸优化问题还要求等式约束都为线性约束(仿射函数)
?
?
?这个问题可以转化为
?
?
?
?
?
? 这里称为松弛变量(slack variable)
- 准凸优化:
- 若目标函数
为凹,则称为非凸问题,不是凹问题
- 若极大化凹函数,则仍是凸问题
- 局部最优,对于凸问题,局部最优即是全局最优
- 可微目标函数最优解的一阶必要条件
最优解<==>
? 从图上看即为最优解处的函数梯度与之间夹角小于等于
°
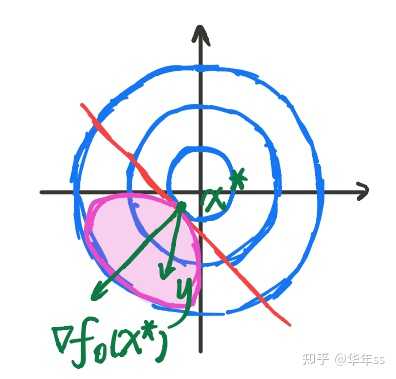
利用一阶最优条件,求解凸优化问题举例
- 例1,约束仅为等式约束
? 带入一阶最优条件
? 令,
? 图上看结果是:最优解处函数梯度垂直于的化零空间
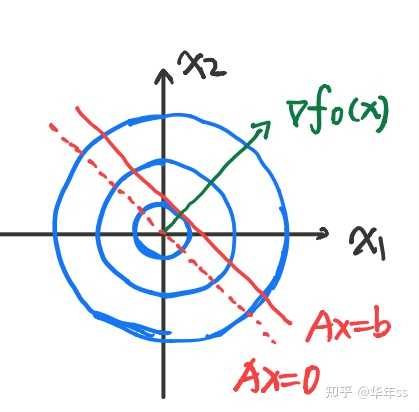
- 例2,约束仅为非负约束
? ①
? 上式是关于的线性函数,若想要大于等于0恒成立,则系数必然
②。
? 当时,①为
③
? 结合②③与原约束,得
。这两项内积为0,且都非负,所以
。注意这里得出了一个重要性质,最优解处,要么梯度值分量为0,要么约束取等号(此处是
分量为0),这个条件叫做互补条件(complementary)。以下图为例检验一下,蓝色线为目标函数等高线,约束为第一象限
,此时满足互补条件。
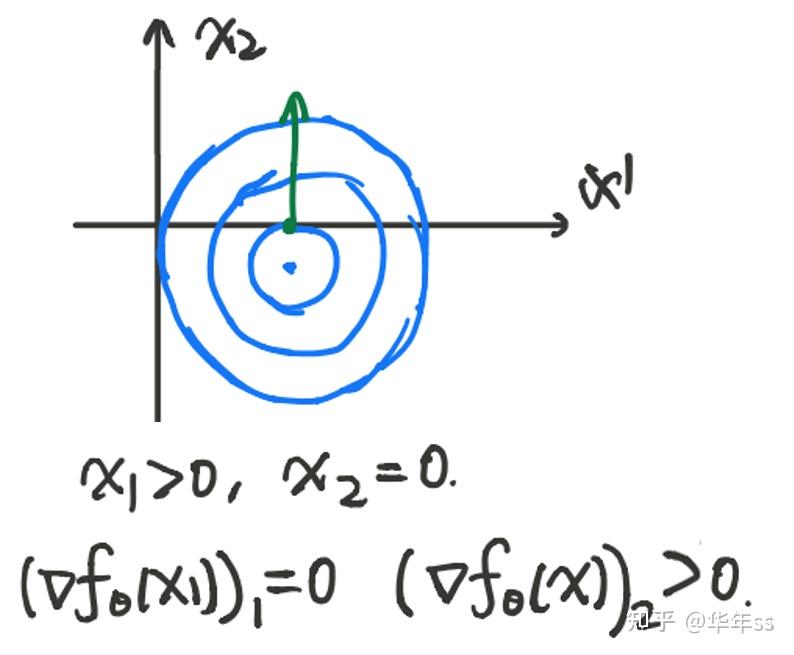
推荐阅读
对于出身数学系的人,建议放弃Boyd,先读完An Easy Path to Convex Analysis and Applications第一章熟悉affine set和relative interior相关概念(后三章相比后面提到的Bertsekas讲得要浅不少,感觉没必要看了):
https://people.scs.carleton.ca/~bertossi/dmbi/material/Convex%20Analysis.pdf
然后再读完Bertsekas的Convex Optimization Theory:
http://web.mit.edu/dimitrib/www/Convex_Theory_Entire_Book.pdf
前者我差不多看完了,读起来通顺,但深度不够。后者看到了第四章一半处,体验是只要挺过第一章(第一章不时有跳步的地方,所以可以搭配这位大佬的notes:Yuchao Li - Notes),后面的内容读起来很畅快。
Boyd我尝试翻看过三次,每次没结束介绍章or第一章就看不下去了,因为实在受不了这种摆上来一句话,然后不给证明让读者自己想的风格。
相关文章: