- 作者:佚名
- 发表时间:2024-07-08 14:57
传统的材料微结构拓扑优化设计,均以材料某一方面或某几方面的极限性能为设计目标,求解在宏观尺度上均匀分布的微结构构型,即周期性“功能”材料设计.20世纪90年代中期,Sigmund首先使用逆向均匀化技术获得具有某些良好特性的复合材料[1, 2].之后,张卫红等[3]提出性能预测与敏度分析效率更高的“能量法”.周期性“功能”材料由于制造成本低、性能优越,已广泛应用于各工业产品,但随着工程发展的要求,“功能性”材料已难于进一步满足多功能、综合性能等要求.因此,基于宏观特性的材料微结构设计逐渐成为研究热点.为了实现基于宏观的微观材料设计,张卫红和孙士平[4]提出材料结构/尺度关联的一体化技术,先进行宏观结构分析,再利用有限元超单元技术实现了基于宏观的非周期性材料设计.文献[5, 6]采用双向渐进结构优化(Bi-directional Evolutionary Structural Optimization,BESO)法对周期性结构分别进行静动态优化,并指出当周期性子结构数增加时,宏观结构快速收敛于材料微观结构[7],实现了基于宏观的周期性材料设计.针对超轻材料中的多孔材料和类桁架材料,Yan等[8, 9]通过均匀化理论建立了宏观结构和微观材料的联系,提出宏观、微观两个尺度并发优化设计的模型与求解方法,并实现了多孔材料动力学结构/材料一体化设计[10].刘远东等[11]通过单元相对密度建立了宏观、微观设计变量的联系,建立了满足静动态力学条件下的金属材料/结构并发优化模型,比较了周期性“功能”材料设计、结构设计的侧重点以及一体化设计的优势.实际上,一体化设计也可以理解为基于宏观的周期性材料设计.热传导问题是拓扑优化应用较早的领域之一.文献[12, 13, 14, 15, 16, 17]分别基于渐进结构优化(Evolutionary Structural Optimization,ESO)法、固体各向同性材料惩罚(Solid Isotropic Material with Penalization,SIMP)微结构模型以及独立连续映射方法讨论了结构热传导问题.刘书田和贺丹[18]基于材料增加的渐进结构优化(Additive Evolutionary Structural Optimization,AESO)方法,进一步提出了材料渐进增加的概念,并讨论该方法在热传导结构拓扑优化中的应用.Gao等[19]以散热弱度为目标函数,基于ESO法提出并解决了热传导问题中载荷的拓扑相关性问题,而张晖等[20]在考虑载荷拓扑相关性同时以温度方差作为目标函数研究了热传导问题.
在以往的基于宏观的微观材料研究中,更多地关注在满足力学性能要求下,多孔材料的宏观排布以及材料微结构的构型,但关于宏观热传导条件对材料微结构构型的影响研究较少.为了研究宏观热传导条件对材料微结构的影响,与以往方法不同,本文拟基于满足宏观热传导条件的周期性结构开展对周期性传热材料的研究.基于变密度法建立周期性传热结构模型.为实现周期性结构,将结构划分为若干相同子区域,并重新分配散热弱度,相当于附加周期性约束.通过求解偏微分方程(Partial Differential Equations,PDE)消除棋盘格及网格依赖性.采用二维结构数值算例,讨论并分析不同子区域个数,不同载荷工况下的材料微结构构型及拓扑优化结果. 1 周期性传热结构建模方法 1.1 基于SIMP的传统传热结构优化建模
已知传热结构的有限元表达式为

式中:K为整体热传导矩阵;T为温度列阵;P为热流率列阵.
根据SIMP插值理论,单元热传导矩阵[15]可写为

式中:ki为单元热传导矩阵;ki0为初始单元热传导矩阵;xi为单元i的相对密度;p为惩罚因子.
建立多工况热传导结构的拓扑优化数学模型为
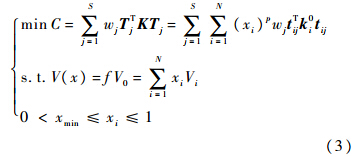
式中:C为结构散热弱度;S为工况数;j为工况号;N为设计域内单元数;wj为工况权系数;tij为单元i的温度列阵;V(x)为优化后结构体积;V0为初始结构体积;Vi为单元i的体积;f为体积比;xmin为密度下限,为防止数值奇异,通常取0.001.
假设热流率与单元相对密度无关,则通过伴随法易推导得
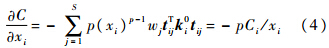
式中:Ci为单元散热弱度.由式(4)可知,敏度可以表达为单元散热弱度的代数运算形式.
常见的拓扑优化求解算法有优化准则(Optimality Criteria,OC)法和数学规划算法两类.优化准则法具有收敛速度快、计算规模和变量数目无关的优点.根据式(4)求解得到敏度后,标准OC法更新设计变量表达式[21]为
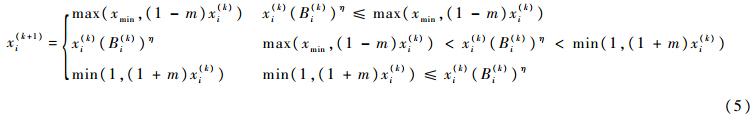
式中:k为第k轮优化迭代过程;m为移动极限;η为阻尼系数,m及η用于确保数值计算稳定性和收敛性,分别取值为0.2和0.5.
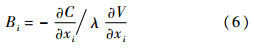
式中: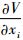 为体积敏度;λ为拉格朗日乘子,根据体积约束方程采用二分法求解.
1.2 克服拓扑优化中的数值不稳定现象
为体积敏度;λ为拉格朗日乘子,根据体积约束方程采用二分法求解.
1.2 克服拓扑优化中的数值不稳定现象
棋盘格现象及网格依赖性问题是连续体拓扑
优化中普遍存在的数值不稳定现象.目前常见的解决办法包括高阶等参元法、周长约束法、全局或局部梯度法、过滤法等[22].敏度过滤法是目前应用最为广泛的方法之一[23].敏度过滤通常可以通过卷积和求解PDE等方式实现.通过卷积进行敏度过滤与求解PDE进行敏度过滤本质上是一致的,但采用有限元方式离散PDE可以使用与结构分析相同的网格信息,相对于搜索式的过滤方式,可以避免占用大量内存,提高过滤效率,适用于大规模优化求解问题[24].
由式(4)可知,敏度取决于单元散热弱度,因此可以通过求解PDE对单元散热弱度过滤来实现敏度过滤.
单元散热弱度过滤后形成的场函数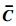 隐含在:
隐含在:
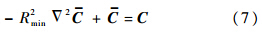
并满足Neumann边界条件:

式中:C为单元散热弱度过滤前形成的场函数;Rmin为PDE参数,其作用类似于卷积敏度过滤中的过滤半径rmin,两者对应关系[24]为

周期性结构的本质就是在各个子区域内具有相同的拓扑形式.对于一个二维设计域问题,如图 1所示,将设计域划分为mx×my个子区域,mx和my分别为沿x轴和y轴的子区域个数.周期性约束的数学模型表达式为
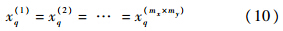
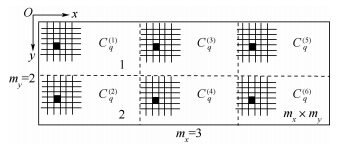 |
| 图 1 周期性结构示意图Fig. 1 Illustration of periodic structure |
式中:上标(1),(2),…,(mx×my)为子区域编号;q=1,2,…,n,其中n=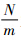 为单个子区域内的有限单元数.
为单个子区域内的有限单元数.
为实现式(10),不同子区域内,相同位置的单元敏度需相等;由式(4)可知,只需进一步满足:
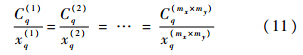
与文献[25]类似,在第 k 轮优化迭代过程中,可以通过重新分配过滤之后的单元散热弱度来实现周期性约束.为了保证当轮优化过程中的目标函数 C 不因周期性约束发生变化,要求分配前后的散热弱度总和不变.
考虑周期性约束的单元散热弱度表达式为
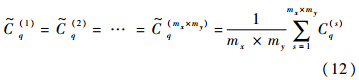
在重新分配单元散热弱度之后,根据式(4)、式(5)来分别计算单元敏度和更新单元相对密度.由于此时每个子区域内同一位置的单元散热弱度相同,即敏度相同,就可以实现周期性结构.
在每轮优化迭代中,采用上述OC算法进行优化求解,直至满足收敛准则:
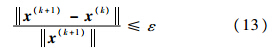
式中:x为由设计变量xi组成的向量.由于过滤的平均作用,优化边界存在着大量的中间密度单元,从而导致优化边界模糊,为了得到清晰的拓扑优化结果,优化过程分两个阶段:第一阶段采用过滤以消除数值不稳定性现象,ε取值为0.5%;在此之后继续采用无过滤方式进行优化直至收敛精度达到0.1%. 2 数值算例及讨论
本节算例均采用平面模型,算例均在MATLAB软件中编程实现[26].用双线性四边形单元离散结构,忽略结构尺寸及材料单位,单元大小为0.25×0.25,在以下算例中,如不特殊说明,材料为各向同性导热材料,p=3,rmin=1.5.随着子区域个数增多,每个子区域内的单元数相应减少,为了严格满足体积比约束,不可避免地,个别单元要取中间值,采用文献[27]中提及的后处理方法显示宏观、微观拓扑构型.
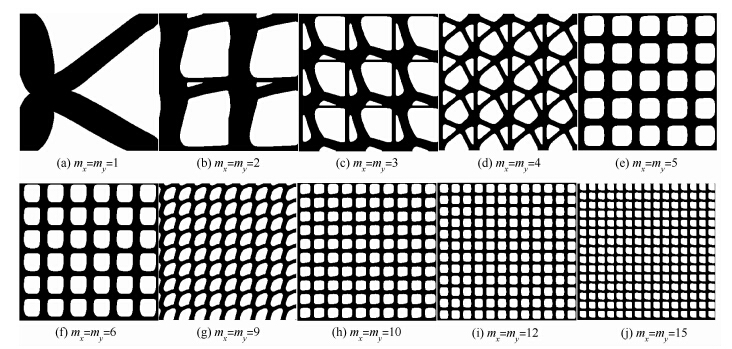
算例1 如图 2所示,平面结构尺寸为180×180,4个角点温度恒为0,设平面结构的左上角为坐标原点,加热点坐标位置为(82,80),热流率为10,导热系数为10.令mn=mx=my,限于篇幅,仅列出mn为1~6、9、10、12、15、36、40、48和60的宏观、微观最优拓扑构型及优化结果.最优拓扑构型如图 3所示.结构散热弱度随mn的变化趋势如图 4 所示,计算得到的规律同样适用于其他算例.
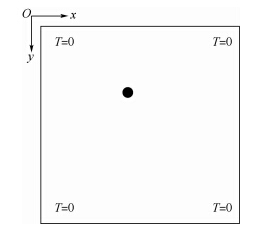 |
| 图 2 数值算例1中受热平面结构示意图Fig. 2 Illustration of heated plane structure in numerical example 1 |
由图 3可知,当子区域个数为1时,即为非周期性结构拓扑优化构型,材料从加热点至冷却点分布,体现了最短传热路径这一特点.由图 4可知,相比较其他子区域个数的最优结构,其散热弱度值最小,说明了非周期性结构拓扑优化结果最优.优化目标总体上随着子区域个数增加而变差,这主要是随着子区域个数增加,单个子区域内的优化空间相应减少,导致宏观周期性结构热传导能力变差.但就本文算例而言,与文献[26]结论有所不同,优化结果呈非严格单调递增性.
 |
| 图 3 数值算例1中不同子区域个数的拓扑优化构型和微结构构型Fig. 3 Optimal topological configurations and microstructure configurations with different numbers of unit cells in numerical example 1 |
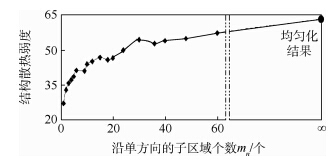 |
| 图 4 数值算例1中散热弱度随子区域个数的变化曲线Fig. 4 Curve of optimal results changing with different numbers of unit cells in numerical example 1 |
当子区域个数不同时,最优拓扑呈现不同的宏观和微观结构.由于宏观结构大小一定,不同的子区域数实际上反映了材料微结构的尺寸,即最优拓扑构型表征了尺寸效应对材料微结构构型的影响.但随着子区域数目不断增加,尽管微观的单胞构型不同,但由其排列而成的宏观结构却逐渐呈现一致性.
如图 5所示的体胞,结构尺寸为1×1,以尺寸a和b为变量,采用均匀化方法得到如图 6所示的宏观、微观结构.
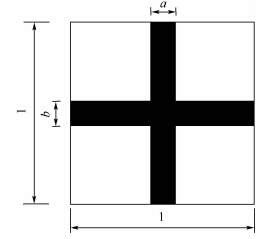 |
| 图 5 均匀化方法表征体胞Fig. 5 Unit cell configuration obtained by homogenization method |
 |
| 图 6 均匀化方法下的宏观、微观结构Fig. 6 Optimal topological configuration and microstructure configuration obtained by homogenization method |
以mn=60为例,材料在x和y方向分布比例为1.89,均匀化结果为1.61,材料分配比例接近.采用均匀化方法得到的散热弱度为62.989 4,由图 4可知,周期性结构散热弱度趋于收敛于均匀化方法计算得到的极限值.
部分情况下,优化结构中出现的细小分支结构会对材料微结构加工制造造成影响,因此该方法在最优结构的可加工性方面需进一步改进.
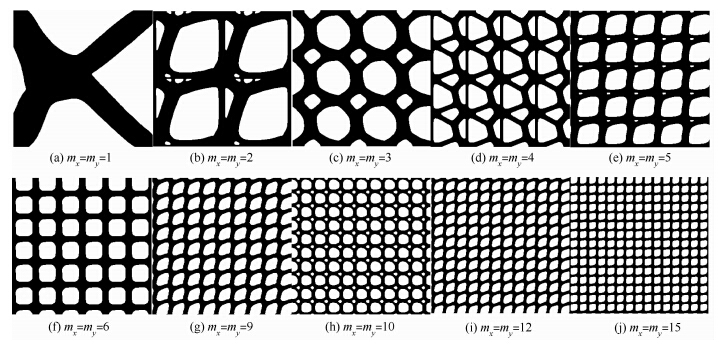
算例2 基本参数如算例1,加热点位置为(30,106),为简单起见,仅列出mn为1~6、9、10、12和15的宏观优化构型,如图 7所示.
 |
| 图 7 数值算例2中不同子区域数个数的拓扑优化构型Fig. 7 Optimal topological configurations with different numbers of unit cells in numerical example 2 |
由图 3、图 7可知,受热方式不同,材料微结构构型有所不同.因此在材料微结构设计时有必要考虑宏观结构受热方式.对于mn=9的情况,从加热点到右下角点没有材料分布,此外,表 1中的数据显示,比较前后情况,其柔顺度值增大,说明了宏观周期性约束有可能会导致拓扑优化结果失去最短传热路径.
| 子区域个数 | 迭代次数 | 最优散热弱度 |
| 6×6 | 68 | 41.032 8 |
| 9×9 | 60 | 47.849 2 |
| 10×10 | 55 | 45.106 5 |
算例3 基本参数同算例1,考虑两个工况且每个工况的加权系数为0.5,加热位置分别在(82,80)和(30,106).仅列出mn为1~6、9、10、12和15的宏观优化构型,如图 8所示.
 |
| 图 8 数值算例3中不同子区域个数的拓扑优化构型Fig. 8 Optimal topological configurations with different numbers of unit cells in numerical example 3 |
由图 3、图 7和图 8比较发现,单、多工况下材料微结构有所不同,表明多目标建模会影响材料微结构构型进而会影响周期性宏观结构. 3 结 论
基于变密度法建立的周期性传热结构可以实现满足宏观导热性能的周期性材料设计,即“结构性”的材料设计.
1) 在设计域内附加周期性约束,通过重新分配单元散热弱度以及基于PDE消除棋盘格和网格依赖性的方法可以实现宏观周期性传热结构设计.
2) 数值实验结果表明,当宏观结构承载方式不同时,微观材料胞元呈现不同的拓扑优化构型.子区域个数不同时,优化得到的不同材料微结构实际上反映了材料的尺寸效应对材料设计的影响,并最终导致周期性结构有所不同.就本文算例而言,当子区域个数不断增加时,优化结果呈非严格单调递增性,且逐渐趋向收敛于均匀化方法对应的极限值.
3) 在优化过程中出现的细小分支结构将会对材料微结构生产加工造成影响,因此结构在可加工性方面需进一步改进. 相关文章: